Scioly.org

But its still a good idea to know the formula for Escape Velocity: (G2M/R)^0.5
You still might want to know basic facts about each of the planets... just saying...

robodude wrote:But its still a good idea to know the formula for Escape Velocity: (G2M/R)^0.5
You still might want to know basic facts about each of the planets... just saying...

uhhh, teach me about 'Escape Velocity' formula because I've never even heard of it.
help

waawamellon wrote:

robodude wrote:But its still a good idea to know the formula for Escape Velocity: (G2M/R)^0.5
You still might want to know basic facts about each of the planets... just saying...

uhhh, teach me about 'Escape Velocity' formula because I've never even heard of it.
help

It's basically the velocity that an object need to have to escape from the gravitational field of another object (such as a planet). So, if a satellite is orbiting a planet, it will break away from it's orbit if it reaches it's escape velocity.

I don't know the formula for it though, so I can't really help you on that.

Escape velocity is the velocity something must be traveling to escape the gravity of a planet. So if I wanted to throw a base ball so hard and fast that it escaped the planet, then I would have to throw it so that the velocity was equal or grater than the escape velocity of the Earth. The formula is only if something is traveling in a straight line, however:

(m2g/r)^0.5
The power to .5 is the same as square root, just FYI.

The square root of m times g time 2, divided by the r, where g= the gravitional constant (6.67*10^-11), r = radius of the planet, and m = planet's mass.

I hope that helps!

actualy, that DID help! thank you!!!!!!!!

Wait, I think I might of gotten something wrong.

If an object escapes the gravitational field of a planet, did it have to reach the escape velocity of the planet or it's own escape velocity?

No. Each planet has its own velocity. It doesn't matter whether you are throwing a baseball, a couch, or a giant building (somehow), they all have to reach the same velocity. Now, you would have to work a lot harder to throw couch than a baseball, but it still has to reach the same velocity. Remeber, size and mass does NOT the gravitational pull on that item! A baseball would fall just as fast as a bowling ball.
Does it make sense now?

robodude wrote:Remeber, size and mass does NOT the gravitational pull on that item! A baseball would fall just as fast as a bowling ball.
Does it make sense now?

Yes and no. For all objects of a reasonable size, their mass is negligible when compared to the mass of say, the Earth, so yes, the gravitational pull isn't really determined by the object's mass.

If you're talking something like the moon on the other hand, it's going to be different, because it has a significant mass.

Newton's Law of Universal Gravitation states that:



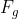
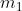
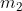
Where is the force of gravity, G is the universal gravitational constant (), and are the masses of the two objects, and r is the distance between their centers of mass.

andrewwski wrote:

robodude wrote:Remeber, size and mass does NOT the gravitational pull on that item! A baseball would fall just as fast as a bowling ball.
Does it make sense now?

Yes and no. For all objects of a reasonable size, their mass is negligible when compared to the mass of say, the Earth, so yes, the gravitational pull isn't really determined by the object's mass.

If you're talking something like the moon on the other hand, it's going to be different, because it has a significant mass.

Newton's Law of Universal Gravitation states that:



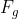
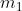
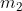
Where is the force of gravity, G is the universal gravitational constant (), and are the masses of the two objects, and r is the distance between their centers of mass.

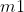
This is correct for force, but not for escape velocity, which is derived by setting the initial kinetic energy equal to the initial gravitational potential energy. The mass of the object cancels. The same is true for acceleration. In both cases drag is left out of the equation, but on an airless world escape velocity and rate of fall will be the same for any two objects regardless of mass, as robodude said.

Ok, so we are all in agreence that to calculate escape velocity, you use where M is the mass of the planet, G is the Gravitational constant, and R is the radius of the planet.