Page 30 of 34
Re: Wind Power B/C
Posted: April 3rd, 2017, 5:54 am
by heiber
heiber wrote:[Resistance changes with length yeah but I think you don't need length in this problem. Resistivity I believe measures resistance per length, but the resistance is given to you so I think the length can safely be ignored.
OK. That helps. We've been trying to find equations and information that include distance. So the distance is included in the resistance calculation. Here is another example from the same test.
21. If a power plant is generating 100 MW, running on a 20 KV line (20 kilometers long), loses 10 MW of power after running along the line, how much resistance does the line have? (2 pts) Their answer:
1) Find Amps: P/V 100MW / 20KV= 5000A
2) Find Ohms: V/I= 20KV / 5MA= 4 ohms
My questions:
From Ohms Law, Resistance = Power / (Current * Current) or 100 MW / (20 KV * 20 KV) = 250 which is different. Why can't you use this equation and why is the answer different from above. All of the equations appear to be coming from the electrical formula wheel so would think it would work out either way.
Again - have information such as power loss of 10 MW and length of 20 kilometers that does not appear to even be used.
Thanks again.[/quote]
Bumping to see if I can get help understanding the solution to this problem. Thanks.
Re: Wind Power B/C
Posted: April 3rd, 2017, 9:42 am
by freed2003
Ummm volts don't measure current
Ionizer wrote:freed2003 wrote:andrewwski wrote:
You're correct that distance is a factor in power loss. For a constant gauge wire, it will have a constant resistivity - or resistance per unit length. So as the length increases, so does the distance.
...
But, if the same gauge line was used, and the resistance was not given, we could determine the resistance. The resistivity of the line is 0.2 ohms/100 km = 0.002 ohm/km. So if the distance was 50 km of the same line, the resistance would be 0.002 ohms/km * 50 km = 0.1 ohm. Then proceed as above.
But to get the resistance from the resistivity won't you also have to know things like the cross section area?
I think there is a misunderstanding here. Resistivity is not resistance per length. Resistivity has units of ohm meters, not ohms per meter. The technique andrewwski describes works, but it's not using resistivity, it's using some other quantity. You can use the resistivity equation to get the same answer through proportions. The cross sectional area will cancel out.
I'm still confused, you said they weren't using resistivity but then said it works? What would the cross section cancel with
Re: Wind Power B/C
Posted: April 3rd, 2017, 2:17 pm
by Ionizer
freed2003 wrote:
I'm still confused, you said they weren't using resistivity but then said it works? What would the cross section cancel with
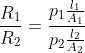
In this case
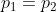
and
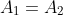
, so
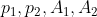
all cancel out, so it turns out you don't need resistivity or cross sectional area to find
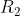
. Once you plug in all your numbers you can just solve for
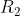
.
Re: Wind Power B/C
Posted: April 5th, 2017, 5:13 pm
by vjindal
Check this out if you need ideas for wind turbines:
https://www.youtube.com/watch?v=603F7vPUbrg
On my setup I got 1850 millivolts.
Re: Wind Power B/C
Posted: April 5th, 2017, 7:30 pm
by freed2003
Nice, what resistor are you on?
Since I didn't want to double post I'll edit this in
33) The power generated by a turbine is 18,000 Watts. If the wind speed, which is initially 30 m/s decreases by 25%, what must the lift force be in order to generate the same amount of power? A) 600 N B) 2,400 N C) 60 N D) 240 N E) 800 N
Can someone help? How would you know the initial lift force?
Re: Wind Power B/C
Posted: April 8th, 2017, 1:53 pm
by maxxxxx
freed2003 wrote:
Since I didn't want to double post I'll edit this in
33) The power generated by a turbine is 18,000 Watts. If the wind speed, which is initially 30 m/s decreases by 25%, what must the lift force be in order to generate the same amount of power? A) 600 N B) 2,400 N C) 60 N D) 240 N E) 800 N
Can someone help? How would you know the initial lift force?
viewtopic.php?f=226&t=9285&start=195#p307423
Re: Wind Power B/C
Posted: April 9th, 2017, 6:19 pm
by vjindal
freed2003 wrote:Nice, what resistor are you on?
Since I didn't want to double post I'll edit this in
33) The power generated by a turbine is 18,000 Watts. If the wind speed, which is initially 30 m/s decreases by 25%, what must the lift force be in order to generate the same amount of power? A) 600 N B) 2,400 N C) 60 N D) 240 N E) 800 N
Can someone help? How would you know the initial lift force?
Thanks!!
Unfortunately its impossible to tell due to the internal resistance of the CD drive. Try it out and see how it is on your setup!
Re: Wind Power B/C
Posted: April 14th, 2017, 7:50 am
by scioly2222
Can someone help confirm the solution for this problem?
A pumped hydroelectric plant has an upper reservoir of water shaped as a cone with a height of 10 meters and a maximum radius of 4.5 meters. The bottom of the reservoir lies 14m above the turbine used at the plant. If the density of the water is 1000 kg/m3 and gravity is 9.81m/s, how much energy is held in the reservoir when full?
Solution approach:
Volume of the cone would be 1/3 * pi * r (squared) * h
Mass of the cone = volume * density
Since center of mass of the code will be 3/4 height -- taking the average height as (14 + 7.5) meters
Energy = m * g * h (multiple all the above with given g)
Wanted to confirm if the key is wrong from this test.
Re: Wind Power B/C
Posted: April 14th, 2017, 7:36 pm
by Alex-RCHS
scioly2222 wrote:Can someone help confirm the solution for this problem?
A pumped hydroelectric plant has an upper reservoir of water shaped as a cone with a height of 10 meters and a maximum radius of 4.5 meters. The bottom of the reservoir lies 14m above the turbine used at the plant. If the density of the water is 1000 kg/m3 and gravity is 9.81m/s, how much energy is held in the reservoir when full?
Solution approach:
Volume of the cone would be 1/3 * pi * r (squared) * h
Mass of the cone = volume * density
Since center of mass of the code will be 3/4 height -- taking the average height as (14 + 7.5) meters
Energy = m * g * h (multiple all the above with given g)
Wanted to confirm if the key is wrong from this test.
That solution certainly looks right to me. I got 44.7 MJ doing what you did.
The only thing I could think of is maybe they meant the cone having the tip at the top? Obviously this wouldn't make sense realistically, but it would give you a different answer: 34.3 MJ.
What did the key say?
Re: Wind Power B/C
Posted: April 14th, 2017, 8:32 pm
by scioly2222
The key said "1040.144 kJ"
Alex-RCHS wrote:scioly2222 wrote:Can someone help confirm the solution for this problem?
A pumped hydroelectric plant has an upper reservoir of water shaped as a cone with a height of 10 meters and a maximum radius of 4.5 meters. The bottom of the reservoir lies 14m above the turbine used at the plant. If the density of the water is 1000 kg/m3 and gravity is 9.81m/s, how much energy is held in the reservoir when full?
Solution approach:
Volume of the cone would be 1/3 * pi * r (squared) * h
Mass of the cone = volume * density
Since center of mass of the code will be 3/4 height -- taking the average height as (14 + 7.5) meters
Energy = m * g * h (multiple all the above with given g)
Wanted to confirm if the key is wrong from this test.
That solution certainly looks right to me. I got 44.7 MJ doing what you did.
The only thing I could think of is maybe they meant the cone having the tip at the top? Obviously this wouldn't make sense realistically, but it would give you a different answer: 34.3 MJ.
What did the key say?