No - it actually does matter how much water you use!
Think about it this way - if you have all water and no air, you have no pressure. Nothing pushing the water out (except gravity, but then there's an equivalent volume of air entering upward at atmospheric pressure) - you won't go anywhere.
If you have all air and no water, you have a greater pressurized volume, but the only mass you are expelling is the mass of that air - you won't go very far.
There will actually be an optimum. You can think of two design variables to the optimization problem as being the pressurized volume and mass of propellant. You then have a constraint - a fixed volume - and thus you really have one degree of freedom - water-to-air ratio, assuming you're pumping to constant pressure.
If you look at the basic rocket equation, you have
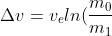)
where
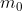
is the initial total mass (including propellant) and
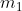
is the dry mass (without propellant). So you could write
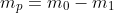
as the mass of the propellant, which allows (1) to be written as:
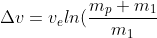)
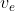
is the escape velocity of the propellant, which will be dependent on the pressure. It's going to be time-varying, as the pressure will be time-varying, but a higher pressure will result in a higher
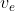
.
We can take Bernoulli's equation, which says that the energy per unit volume must be conserved. For a single fluid:
where
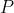
is pressure,
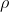
is density of the fluid, and

is velocity of the fluid. So, in our case, let's take state (1) to be the inside of the pressure vessel, where we have no velocity, and state (2) to be the edge of the nozzle, where pressure is ambient (gauge pressure is zero), and the fluid is moving out with escape velocity. So this reduces to:
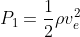
Now, of course, we lose pressure in the vessel as air is lost, so this
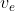
is time varying, but you can see that it depends on the pressure.
Since the equation for the change in velocity - which is the quantity we want to optimize - is nonlinear, then we see that the ratio of water to air in the bottle
does matter, as there is a ratio which will maximize
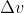
.
We could further compute this theoretically by writing Bernoulli's equation for two fluids, writing a differential equation for the change in pressure over time, and then integrating over time, but it's probably easier to test it yourself by varying the amount of water.