Scioly.org

That's exactly what i did (for the $ 17.71 i mean). First off if you've had experience taking AMC and other related contests, you would know number theory and such (at least the basics) is a fairly big portion of the test.

And there really aren't too many other efficient ways to solve it (another member of our math team tried the different options until he got the one that made sense, an advantage of the multiple choice format of the AMC).

Speaking of math team members, it has come to my understanding that many schools actually offer this test to the whole school? At our school, our math team coach just orders the stuff and we take it after school on the day of the test. How many kids from your schools qualified? Our schools only ever had 2 qualifiers before me, about 3 years ago...and this year im the only one.

@Winneratlife: Did you get #25??? Niceeee, and i'd love the solution...honestly the problem just blew my mind, i haven't seen something that difficult on the first 10 of AIME. Of course, it was combinatorial geometry. Probably the two most dreaded subjects put together into one absolutely mind boggling question....how long did you take to solve it?

lllazar wrote:Speaking of math team members, it has come to my understanding that many schools actually offer this test to the whole school? At our school, our math team coach just orders the stuff and we take it after school on the day of the test. How many kids from your schools qualified? Our schools only ever had 2 qualifiers before me, about 3 years ago...and this year im the only one.

I'm generally the only qualifier through the 10; we get a couple kids who qualify through the 12 each year though. I also would have been the only JMO qualifier last year; my school's never had one.

We normally get AIME qualifiers every year, but never USAMO/JMO.

I don't know about the "whole school" deal; we don't do it and it seems rather expensive; I'm sure some schools like TJ do though.

Umm... forgive my ignorance and all, but what does AMC stand for? Furthermore, what is it?

prelude to death wrote:Umm... forgive my ignorance and all, but what does AMC stand for? Furthermore, what is it?

American Math Competition

It's run by the MAA in an attempt to expose more kids to math competitions, improve problem solving skills, and select the USA IMO team.

Ok.
I should have realized that we would have needed to plug in numbers. (:
I'm guessing that I got 14-ish right, but that's a stretch in itself. Well, next year I'll be taking AMC 12. Whoot, fun.

Okay, thanks for the clarification, because I didn't know what it was.... >.<

Don't feel bad, i didn't know what it was till last spring. My middle school didn't even have a mathcounts team. As far as actually doing math because i like it, and not slogging through the boring school curriculum, i'd have to say i didn't actually start until last fall. Sucks for me

But ya, as far as MC and AMC and other "Problem solving" type math competitions go, how early you start has a huge impact on how well you end up doing. It's like learning a language, kids learn languages way more easily when they are really young.

@winneratlife: Ya i'd think it would be really expensive...my friend goes to Cedar Shoals high school in California, and they have on average 6-7 USAMO qualifiers each year....insanity!!!

My school offers AMC to the whole school, but we only end up having like 25 people (total) who take it. We've probably had some AIME qualifiers, but I don't think we've had anyone go to USAMO/JMO. I'm still sorta nervous waiting for the results to come back because my score's right on the cutoff for AIME.

Winneratlife: If you have full solutions, by all means post them. I really want to see how to do 20 and 25.

Alpha Tauri, for number 20:

First of all, note that a chord of length in a circle of radius intersects an arc of measure degrees. Why? Draw chord of length and draw the radii to the the two endpoints of said chord. You get an equilateral triangle.

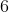
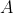
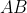
Next, note that if you were to draw consecutive chords of length in the circle mentioned, you'd make a regular hexagon with side length . If you pick one vertex of this hexagon, then the question is asking you what's the probability that the next point on the circle you pick will intersect the clockwise chord of length from vertex, let's just call it, of the hexagon (that chord is ). Now the questions is obvious. 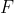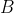If you pick any point between the vertices and of the hexagon, the clockwise chord of length from that set of points will intersect chord . 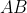The possibility of selecting a point on minor arc is clearly . (Does that make sense?)

If not, draw everything out as i mentioned and go through the steps of the "proof" above.

Ohh, I get it now. That's much simpler than I thought it'd be...I guess I got confused by the wording of the question.