Unome wrote:Note, the Nationals test is generally significantly harder than the MIT test, though not as hard as the Princeton test.
The Princeton test was definitely on the extreme end of the difficulty spectrum. It turned out both harder and longer than I intended.
Unome wrote:The Nationals test also uses obscure knowledge in application-based question, as opposed to how Princeton was more about spitting out obscure knowledge (most of which were directly from Wikipedia, so it shouldn't have been too hard if you had a laptop).
The first section (roughly 30% of the points) was trivia. Pretty much all the questions were also taken directly from Wikipedia, mainly to make the trivia somewhat reasonable (as in, not found in the middle of some obscure astrophysics paper). Basically every astronomy test is very trivia-heavy; my reasoning for this section was that, instead of the top few teams being decided by which ones got the two obscure trivia questions right, there would be a larger number of these trivia questions that top teams are not guaranteed to reduce this effect. I guess a common pitfall would have been for teams to spend too much time being stuck on the section.
The second section (roughly 30% of the points) was much more similar to the Nationals test. It was supposed to be essentially the Nationals test minus any calculations (for those of you who don't like calculations). I think the score distribution here was similar to that at Nationals (correcting for team skill).
The third section (roughly 30% of the points) was pure application and calculation. Since the calculations required applying concepts (hence knowing the concepts well) and difficult math, very few teams made any progress at all. Aside from the last two pages (which were a bit unreasonable), the tasks required a deeper understanding of both concepts and the physics behind the calculations than those on the Nationals test (which are pretty dry, IMO) - the concepts and physics should be known to a top-tier team, but synthesizing them would be difficult. However, this was clearly too much to do in the time given. There's also a reason why very few astronomy tests have in-depth 'use concepts to solve a problem' questions - because they're usually way too hard.
The fourth section (roughly 10% of the points) was an visual assessment of familiarity with stellar evolution.
Next year, the test will probably be less of (concept trivia, calculation applications) and more of (concept applications, calculation trivia), which should be a much better experience for teams. For instance, a problem based on
Unome wrote:Question: why do higher-mass stars have the radiative layer outside the convective layer while low(er) mass stars are the opposite?
Adi1008 wrote:Greater mass means greater pressures and temperatures at the center of the star, creating a large temperature gradient between the core and the outer layers - this results in convection. Furthermore, the outer layers have a very low density, so energy flows through them more efficiently by radiation
would probably be extended to ask:
Q. Why does a greater core temperature create a large temperature gradient?
A. Because the CNO cycle begins to dominate at 17 MK (the Sun's core is 15 MK). Note that pressure does not really matter here.
Q. Why does the CNO cycle cause a large temperature gradient?
A. The energy produced by the CNO cycle is roughly proportional to
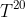
, while that produced by the p-p chain is only roughly
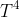
.
Q. Why? lul
A. The way non-resonant reactions (quantum tunneling) works (look at the atomic masses of the limiting reaction components).
Q. What about the shell?
A. The dependence is more closely related to opacity than density (at least it's usually better to think in terms of opacity). Opacity also has temperature dependence rules, which depend on what source of opacity is dominant.
Q. What type of stars are fully convective?
A. Those on the Hayashi track.
Q. What is the relationship between temperature, mass, and radius along the Hayashi track? You may make practical assumptions. glhf
A. [outline] It's adiabatic, and assuming ideal gas we can approximate by polytrope (
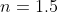
); plugging
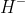
opacity, we can solve for stuff on the surface; combining and doing lots of math we get something like
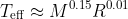
. There's also some metallicity dependence, but w/e.