Circuit Lab B/C
-
mjcox2000
- Member

- Posts: 121
- Joined: Fri May 09, 2014 3:34 am
- Division: Grad
- State: VA
- Has thanked: 0
- Been thanked: 0
Re: Circuit Lab B/C
To revive this thread:
Diagram: https://drive.google.com/file/d/1-IqHS7 ... sp=sharing
Resistors R1, R2, and R3, voltage source V1, and current source I1 are arranged as in the diagram. These circuit elements have the following values:
R1: 5Ω
R2: 3Ω
R3: 10Ω
V1: 8V
I1: 6A
What is the voltage across and current through each of the three resistors?
Diagram: https://drive.google.com/file/d/1-IqHS7 ... sp=sharing
Resistors R1, R2, and R3, voltage source V1, and current source I1 are arranged as in the diagram. These circuit elements have the following values:
R1: 5Ω
R2: 3Ω
R3: 10Ω
V1: 8V
I1: 6A
What is the voltage across and current through each of the three resistors?
MIT ‘23
TJHSST ‘19
Longfellow MS
See my user page for nationals medals and event supervising experience.
TJHSST ‘19
Longfellow MS
See my user page for nationals medals and event supervising experience.
-
Cathy-TJ
- Member

- Posts: 28
- Joined: Sun Jan 20, 2019 7:13 pm
- Division: C
- State: VA
- Has thanked: 0
- Been thanked: 0
Re: Circuit Lab B/C
mjcox2000 wrote:To revive this thread:
Diagram: https://drive.google.com/file/d/1-IqHS7 ... sp=sharing
Resistors R1, R2, and R3, voltage source V1, and current source I1 are arranged as in the diagram. These circuit elements have the following values:
R1: 5Ω
R2: 3Ω
R3: 10Ω
V1: 8V
I1: 6A
What is the voltage across and current through each of the three resistors?
Voltages: R1: 65/9 V (Right is positive) R2: 41/3 V (Bottom is positive) R3: 130/9 V (Right is positive) Currents: R1: 13/9 A (Right to Left) R2: 41/9 A (Bottom to Top) R3: 13/9A (Bottom to Top) Edited because oops
Nationals Placings:
2019 Circuit Lab - 1
2018 Disease Detectives - 1
2015 Picture This - 6
2019 Events:
Chemistry Lab, Circuit Lab, Disease Detectives
Competitors today, teammates tomorrow
2019 Circuit Lab - 1
2018 Disease Detectives - 1
2015 Picture This - 6
2019 Events:
Chemistry Lab, Circuit Lab, Disease Detectives
Competitors today, teammates tomorrow
-
mjcox2000
- Member

- Posts: 121
- Joined: Fri May 09, 2014 3:34 am
- Division: Grad
- State: VA
- Has thanked: 0
- Been thanked: 0
Re: Circuit Lab B/C
That looks right! (Although, if this were a test, you might want to evaluate those fractions and truncate them to 1 sig fig.) Your turn!Cathy-TJ wrote:mjcox2000 wrote:To revive this thread:
Diagram: https://drive.google.com/file/d/1-IqHS7 ... sp=sharing
Resistors R1, R2, and R3, voltage source V1, and current source I1 are arranged as in the diagram. These circuit elements have the following values:
R1: 5Ω
R2: 3Ω
R3: 10Ω
V1: 8V
I1: 6A
What is the voltage across and current through each of the three resistors?Voltages: R1: 65/9 V (Right is positive) R2: 41/3 V (Bottom is positive) R3: 130/9 V (Right is positive) Currents: R1: 13/9 A (Right to Left) R2: 41/9 A (Bottom to Top) R3: 13/9A (Bottom to Top) Edited because oops
MIT ‘23
TJHSST ‘19
Longfellow MS
See my user page for nationals medals and event supervising experience.
TJHSST ‘19
Longfellow MS
See my user page for nationals medals and event supervising experience.
-
Cathy-TJ
- Member

- Posts: 28
- Joined: Sun Jan 20, 2019 7:13 pm
- Division: C
- State: VA
- Has thanked: 0
- Been thanked: 0
Re: Circuit Lab B/C
Hi!
Write and simplify a boolean algebra expression for the following diagram:
(A link longer than my attention span)
http://www.101computing.net/logic-gates ... itle=Title
For fun, make a truth table.
Write and simplify a boolean algebra expression for the following diagram:
(A link longer than my attention span)
http://www.101computing.net/logic-gates ... itle=Title
For fun, make a truth table.
Nationals Placings:
2019 Circuit Lab - 1
2018 Disease Detectives - 1
2015 Picture This - 6
2019 Events:
Chemistry Lab, Circuit Lab, Disease Detectives
Competitors today, teammates tomorrow
2019 Circuit Lab - 1
2018 Disease Detectives - 1
2015 Picture This - 6
2019 Events:
Chemistry Lab, Circuit Lab, Disease Detectives
Competitors today, teammates tomorrow
-
mjcox2000
- Member

- Posts: 121
- Joined: Fri May 09, 2014 3:34 am
- Division: Grad
- State: VA
- Has thanked: 0
- Been thanked: 0
Re: Circuit Lab B/C
Cathy-TJ wrote:Hi!
Write and simplify a boolean algebra expression for the following diagram:
(A link longer than my attention span)
http://www.101computing.net/logic-gates ... itle=Title
For fun, make a truth table.
A' OR B' OR C Truth table: [code]A|B|C|Result 0|0|0|1 0|0|1|1 0|1|0|1 0|1|1|1 1|0|0|1 1|0|1|1 1|1|0|0 1|1|1|1[/code]
MIT ‘23
TJHSST ‘19
Longfellow MS
See my user page for nationals medals and event supervising experience.
TJHSST ‘19
Longfellow MS
See my user page for nationals medals and event supervising experience.
-
Cathy-TJ
- Member

- Posts: 28
- Joined: Sun Jan 20, 2019 7:13 pm
- Division: C
- State: VA
- Has thanked: 0
- Been thanked: 0
Re: Circuit Lab B/C
That was my answer! You got the next question!mjcox2000 wrote:Cathy-TJ wrote:Hi!
Write and simplify a boolean algebra expression for the following diagram:
(A link longer than my attention span)
http://www.101computing.net/logic-gates ... itle=Title
For fun, make a truth table.A' OR B' OR C Truth table: [code]A|B|C|Result 0|0|0|1 0|0|1|1 0|1|0|1 0|1|1|1 1|0|0|1 1|0|1|1 1|1|0|0 1|1|1|1[/code]
Nationals Placings:
2019 Circuit Lab - 1
2018 Disease Detectives - 1
2015 Picture This - 6
2019 Events:
Chemistry Lab, Circuit Lab, Disease Detectives
Competitors today, teammates tomorrow
2019 Circuit Lab - 1
2018 Disease Detectives - 1
2015 Picture This - 6
2019 Events:
Chemistry Lab, Circuit Lab, Disease Detectives
Competitors today, teammates tomorrow
-
mjcox2000
- Member

- Posts: 121
- Joined: Fri May 09, 2014 3:34 am
- Division: Grad
- State: VA
- Has thanked: 0
- Been thanked: 0
Re: Circuit Lab B/C
Diagram: https://drive.google.com/file/d/1pqa8dq ... sp=sharing
Note: this problem requires calculus. (It's possible there's a particularly clever solution that bypasses the calculus, but I can't think of one.)
You are an electrical engineer tasked with charging a capacitor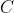 , which is connected in series with resistor
, which is connected in series with resistor 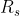 and in parallel with resistor
and in parallel with resistor 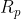 . You want to charge the capacitor to a final voltage
. You want to charge the capacitor to a final voltage 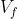 , and you have at your disposal a current source
, and you have at your disposal a current source 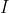 . (See the diagram for the circuit configuration, and note that at time
. (See the diagram for the circuit configuration, and note that at time 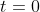 , the capacitor is fully discharged. Also note that
, the capacitor is fully discharged. Also note that 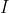 is constant; i.e. the current cannot vary with time.)
is constant; i.e. the current cannot vary with time.)
In the aim of efficiency, you want to dissipate as little power as possible in the resistors as you charge the capacitor to voltage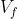 . However, your colleague, who designed the circuit with
. However, your colleague, who designed the circuit with 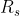 ,
, 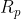 , and
, and 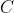 and chose the value of
and chose the value of 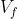 , won't let you change any of those values. The only value you can play around with is the charging current
, won't let you change any of those values. The only value you can play around with is the charging current 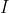 .
.
a) Find an equation, in terms of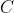 ,
, 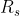 ,
, 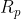 , and
, and 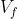 , and
, and 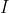 , for the time
, for the time  at which the capacitor is fully charged to voltage
at which the capacitor is fully charged to voltage 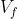 .
.
b) Find an equation, in terms of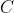 ,
, 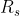 ,
, 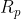 , and
, and 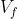 , and
, and 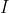 , for the amount of power dissipated in the resistors in the course of charging the capacitor to voltage
, for the amount of power dissipated in the resistors in the course of charging the capacitor to voltage 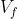 .
.
c) Find an equation, in terms of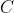 ,
, 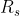 ,
, 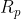 , and
, and 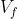 , for the value of
, for the value of 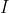 that offers minimum power dissipation. (I'm not convinced this part has a closed-form solution -- if not, do what you can.)
that offers minimum power dissipation. (I'm not convinced this part has a closed-form solution -- if not, do what you can.)
Note: this problem requires calculus. (It's possible there's a particularly clever solution that bypasses the calculus, but I can't think of one.)
You are an electrical engineer tasked with charging a capacitor
In the aim of efficiency, you want to dissipate as little power as possible in the resistors as you charge the capacitor to voltage
a) Find an equation, in terms of
b) Find an equation, in terms of
c) Find an equation, in terms of
MIT ‘23
TJHSST ‘19
Longfellow MS
See my user page for nationals medals and event supervising experience.
TJHSST ‘19
Longfellow MS
See my user page for nationals medals and event supervising experience.
-
UTF-8 U+6211 U+662F
- Exalted Member

- Posts: 1597
- Joined: Sun Jan 18, 2015 7:42 am
- Division: C
- State: PA
- Has thanked: 6 times
- Been thanked: 15 times
Re: Circuit Lab B/C
mjcox2000 wrote:Diagram: https://drive.google.com/file/d/1pqa8dq ... sp=sharing
Note: this problem requires calculus. (It's possible there's a particularly clever solution that bypasses the calculus, but I can't think of one.)
You are an electrical engineer tasked with charging a capacitor, which is connected in series with resistor
and in parallel with resistor
. You want to charge the capacitor to a final voltage
, and you have at your disposal a current source
. (See the diagram for the circuit configuration, and note that at time
, the capacitor is fully discharged. Also note that
is constant; i.e. the current cannot vary with time.)
In the aim of efficiency, you want to dissipate as little power as possible in the resistors as you charge the capacitor to voltage. However, your colleague, who designed the circuit with
,
, and
and chose the value of
, won't let you change any of those values. The only value you can play around with is the charging current
.
a) Find an equation, in terms of,
,
, and
, and
, for the time
at which the capacitor is fully charged to voltage
.
b) Find an equation, in terms of,
,
, and
, and
, for the amount of power dissipated in the resistors in the course of charging the capacitor to voltage
.
c) Find an equation, in terms of,
,
, and
, for the value of
that offers minimum power dissipation. (I'm not convinced this part has a closed-form solution -- if not, do what you can.)
a)
[math]Q=CV[/math]
[math]I_C=C \cdot \frac{dV}{dt}[/math]
[math]I-VR_p = C \cdot \frac{dV}{dt}[/math]
[math]dt = C \cdot \frac{dV}{I-VR_p}[/math]
[math]t + C_{int} = C \cdot -\frac{\ln(I-VR_p)}{R_p}[/math] (the constant of integration also being a C makes this slightly confusing)
[math]t = \frac{-C\ln(I-VR_p)}{R_p} + k[/math] (so I changed it to a k)
[math]t = \frac{-C\ln(I-VR_p) + C\ln I}{R_p}[/math] (but plugging in (0,0) gives us a value for k)
[math]\boxed{t_f = \frac{-C\ln(I-V_fR_p) + C\ln I}{R_p}}[/math]
b) I'm going to assume you mean energy for the next problem?
[math]P = I^2R_s + \frac{V^2}{R_p}[/math]
[math]E = I^2R_s \frac{-C\ln(I-V_fR_p) + C\ln I}{R_p} + \int\frac{V^2}{R_p}dt[/math]
Noting that [math]\frac{dV}{dt} = \frac{I-VR_p}{C}[/math], so [math]dt = \frac{CdV}{I-VR_p}[/math]
[math]\boxed{E = I^2R_s \frac{-C\ln(I-V_fR_p) + C\ln I}{R_p} + \int^{\frac{-C\ln(I-V_fR_p) + C\ln I}{R_p}}_0\frac{CV^2}{IR_p-VR^2_p}dV}[/math]
This technically satisfies what you asked for, but it's really ugly, so I'm guessing I either did it wrong or missed something.
c) I feel like you're supposed to take the derivative of part B with respect to I for this but since I got something weird for part B, I'm going to call it a night.-
mjcox2000
- Member

- Posts: 121
- Joined: Fri May 09, 2014 3:34 am
- Division: Grad
- State: VA
- Has thanked: 0
- Been thanked: 0
Re: Circuit Lab B/C
UTF-8 U+6211 U+662F wrote:mjcox2000 wrote:Diagram: https://drive.google.com/file/d/1pqa8dq ... sp=sharing
Note: this problem requires calculus. (It's possible there's a particularly clever solution that bypasses the calculus, but I can't think of one.)
You are an electrical engineer tasked with charging a capacitor, which is connected in series with resistor
and in parallel with resistor
. You want to charge the capacitor to a final voltage
, and you have at your disposal a current source
. (See the diagram for the circuit configuration, and note that at time
, the capacitor is fully discharged. Also note that
is constant; i.e. the current cannot vary with time.)
In the aim of efficiency, you want to dissipate as little power as possible in the resistors as you charge the capacitor to voltage. However, your colleague, who designed the circuit with
,
, and
and chose the value of
, won't let you change any of those values. The only value you can play around with is the charging current
.
a) Find an equation, in terms of,
,
, and
, and
, for the time
at which the capacitor is fully charged to voltage
.
b) Find an equation, in terms of,
,
, and
, and
, for the amount of power dissipated in the resistors in the course of charging the capacitor to voltage
.
c) Find an equation, in terms of,
,
, and
, for the value of
that offers minimum power dissipation. (I'm not convinced this part has a closed-form solution -- if not, do what you can.)
a) [math]Q=CV[/math] [math]I_C=C \cdot \frac{dV}{dt}[/math] [math]I-VR_p = C \cdot \frac{dV}{dt}[/math] [math]dt = C \cdot \frac{dV}{I-VR_p}[/math] [math]t + C_{int} = C \cdot -\frac{\ln(I-VR_p)}{R_p}[/math] (the constant of integration also being a C makes this slightly confusing) [math]t = \frac{-C\ln(I-VR_p)}{R_p} + k[/math] (so I changed it to a k) [math]t = \frac{-C\ln(I-VR_p) + C\ln I}{R_p}[/math] (but plugging in (0,0) gives us a value for k) [math]\boxed{t_f = \frac{-C\ln(I-V_fR_p) + C\ln I}{R_p}}[/math] b) I'm going to assume you mean energy for the next problem? [math]P = I^2R_s + \frac{V^2}{R_p}[/math] [math]E = I^2R_s \frac{-C\ln(I-V_fR_p) + C\ln I}{R_p} + \int\frac{V^2}{R_p}dt[/math] Noting that [math]\frac{dV}{dt} = \frac{I-VR_p}{C}[/math], so [math]dt = \frac{CdV}{I-VR_p}[/math] [math]\boxed{E = I^2R_s \frac{-C\ln(I-V_fR_p) + C\ln I}{R_p} + \int^{\frac{-C\ln(I-V_fR_p) + C\ln I}{R_p}}_0\frac{CV^2}{IR_p-VR^2_p}dV}[/math] This technically satisfies what you asked for, but it's really ugly, so I'm guessing I either did it wrong or missed something. c) I feel like you're supposed to take the derivative of part B with respect to I for this but since I got something weird for part B, I'm going to call it a night.
your third equation should have [math]I-\frac{V}{R_p}[/math], not [math]I-VR_p[/math], and that error messed up almost everything else you have. With that fix, you would have gotten part a right, and I haven't evaluated part b, but the way you approach it seems reasonable. Wolfram Alpha or Mathematica might help with the more involved integrals.MIT ‘23
TJHSST ‘19
Longfellow MS
See my user page for nationals medals and event supervising experience.
TJHSST ‘19
Longfellow MS
See my user page for nationals medals and event supervising experience.
-
UTF-8 U+6211 U+662F
- Exalted Member

- Posts: 1597
- Joined: Sun Jan 18, 2015 7:42 am
- Division: C
- State: PA
- Has thanked: 6 times
- Been thanked: 15 times
Re: Circuit Lab B/C
Agh! Well that sucks.mjcox2000 wrote:your third equation should have [math]I-\frac{V}{R_p}[/math], not [math]I-VR_p[/math], and that error messed up almost everything else you have. With that fix, you would have gotten part a right, and I haven't evaluated part b, but the way you approach it seems reasonable. Wolfram Alpha or Mathematica might help with the more involved integrals.
a)
[math]Q=CV[/math]
[math]I_C=C \cdot \frac{dV}{dt}[/math]
[math]I-\frac{V}{R_p} = C \cdot \frac{dV}{dt}[/math]
[math]dt = C \cdot \frac{dV}{I-\frac{V}{R_p}}[/math]
[math]t + C_{int} = -CR_p\ln(I-\frac{V}{R_p})[/math] (the constant of integration also being a C makes this slightly confusing)
[math]t = -CR_p\ln(I-\frac{V}{R_p}) + k[/math] (so I changed it to a k)
[math]t = -CR_p\ln(I-\frac{V}{R_p}) + CR_p\ln I[/math] (but plugging in (0,0) gives us a value for k)
[math]\boxed{t_f = -CR_p\ln(I-\frac{V_f}{R_p}) + CR_p\ln I}[/math]
b) I'm going to assume you mean energy for the next problem?
[math]P = I^2R_s + \frac{V^2}{R_p}[/math]
[math]E = I^2R_s \cdot (-CR_p\ln(I-\frac{V_f}{R_p}) + CR_p\ln I) + \int^{t_f}_0\frac{V^2}{R_p}dt[/math]
Now, let's solve for V in terms of t...
[math]t = -CR_p\ln(I-\frac{V}{R_p}) + CR_p\ln I[/math]
[math]\frac{CR_p\ln I - t}{CR_p} = \ln(I-\frac{V}{R_p})[/math]
[math]\ln I - \frac{t}{CR_p} = \ln(I-\frac{V}{R_p})[/math]
[math]Ie^{-\frac{t}{CR_p}} = I - \frac{V}{R_p}[/math]
[math]V = IR_p(1-e^{-\frac{t}{CR_p}})[/math]
[math]E = CI^2R_pR_s\ln\frac{I}{I-\frac{V_f}{R_p}} + \int^{t_f}_0\frac{(IR_p(1-e^{-\frac{t}{CR_p}}))^2}{R_p}dt[/math]
[math]E = CI^2R_pR_s\ln\frac{I}{I-\frac{V_f}{R_p}} + I^2R_p\int^{t_f}_0(1-e^{-\frac{t}{CR_p}})^2dt[/math]
[math]E = CI^2R_pR_s\ln\frac{I}{I-\frac{V_f}{R_p}} + I^2R_p\left[t+\frac{e^{-2\frac{t}{CR_p}}-4e^{{-\frac{t}{CR_p}}}}{-\frac{2}{CR_p}}\right]^{t_f}_0[/math]
[math]\boxed{E = CI^2R_pR_s\ln\frac{I}{I-\frac{V_f}{R_p}} + I^2R_p\left(-CR_p\ln(I-\frac{V_f}{R_p}) + CR_p\ln I+\frac{\frac{(I-\frac{V_f}{R_p})^2}{I^2}-4\frac{I-\frac{V_f}{R_p}}{I}}{-\frac{2}{CR_p}}-\frac{3CR_p}{2}\right)}[/math]
For part c:
[math]\boxed{0 = \frac{d}{dV}\left[CI^2R_pR_s\ln\frac{I}{I-\frac{V_f}{R_p}} + I^2R_p\left(-CR_p\ln(I-\frac{V_f}{R_p}) + CR_p\ln I+\frac{\frac{(I-\frac{V_f}{R_p})^2}{I^2}-4\frac{I-\frac{V_f}{R_p}}{I}}{-\frac{2}{CR_p}}-\frac{3CR_p}{2}\right)\right]}[/math]
Although you'd need to test all of the roots and see which one yields the lowest value
